ANOVA from scratch
Project developed for the “Computer methods” course in the Master in Methodology for behavioral sciences. Full description and examples can be found here and here.
Main function
ANOVA: Perform a one- or two-way fixed-effects ANOVA.
-
Arguments:
-
factor: character vector of length 1 or 2 with the name of the predictors or factors. They must refer to a variable of type factor of a dataframe. In case the factor(s) are not of type factor, the function check_factor is called to transform the dataframe variables into factor type.
-
vd: character vector of length 1 with the name of the outcome or dependent variable. It must refer to a numeric variable of a dataframe.
-
data: dataframe containing the factor or factors and the dependent variable.
-
-
output:
Depending on the number of factors, returns the function one_way or the function two_way.
ANOVA <- function(factor,vd,data){
num_fact <- length(factor)
data <- check_factor(factor,data)
switch(num_fact,
return(one_way(num_fact,factor,vd,data)),
return(two_way(num_fact,factor,vd,data)))
}
Auxiliary functions
check_factor: Checks that the predictors are type factor. If they are not, it transforms the variables into factors in the original dataframe itself and returns it.
check_factor <- function(vars,df){
for (var in vars){
if (!(is.factor(df[,var])))
warning(paste0('se convertira ',var,' en tipo factor '))
df[,var] <- as.factor(df[,var])
}
return(df)
}
anova_plot: Returns line graph with means for each level (one-way ANOVA) or for each combination of levels (two-way ANOVA). Allows exploration of the interaction effect by visual inspection.
anova_plot <- function(num_fact,factor,vd,data,medias=NULL,J=NULL){
if(num_fact==1){
labels <- levels(data[,factor])
plot(1:J,medias,
type='o', lwd=2,
ylim=c(min(data[,vd]),max(data[,vd])),
xlab=factor,ylab=vd,
pch=19, col='#ff6b6b',
xaxt='n')
axis(1,1:J,labels=labels) # xticks
}
else{
interaction.plot(x.factor = data[,factor[1]], trace.factor = data[,factor[2]],
response = data[,vd], fun = mean,
type = "b", legend = TRUE, lwd=2,
ylim=c(min(data[,vd]),max(data[,vd])),
xlab = factor[1], ylab=vd,trace.label=NULL,
pch=c(1,19), col = c('#4ecdc4', '#ff6b6b'))
}
grid(col = "lightgray", lty = "dotted",
lwd = par("lwd"), equilogs = TRUE) # rejilla para ver mejor
}
one_way : Perform one-way fixed-effects ANOVA. The procedure is based on the chapter on one-way ANOVA in Pardo and San Martín (2015). The function provides a list with three dataframes containing the value of the F statistic, its critical level and three measures of effect size.
one_way <- function(num_fact,factor,vd,data){
N <- nrow(data) # Tamaño muestral
J <- nlevels(data[,factor]) # Número de niveles del factor A
# ------------------------------------------------- Estimador variabilidad intra basado
# en varianzas de cada nivel j del factor
varianzas <- aggregate(data[vd],
by=list(data[[factor]]),
FUN=var)[[vd]]
n <- aggregate(data[vd],
by=list(data[[factor]]),
FUN=length)[[vd]]
SCE <- sum((n-1)*varianzas)
glE <- N-J
MCE <- SCE/glE
# ------------------------------------------------- Estimador variabilidad inter
# basado en las medias del factor
medias_A_df <- aggregate(data[vd],
by=list(data[[factor]]),
FUN=mean)
medias_A <- medias_A_df[[vd]] # el df es para la salida
media_tot <- mean(data[,vd])
SCI <- sum( n * (medias_A-media_tot)^2 )
glI <- J-1
MCI <- SCI/glI
F_stat <- MCI/MCE
p_val <- 1-pf(F_stat,glI,glE)
# ------------------------------------------------- Salida
anova_plot(num_fact,factor,vd,data,medias_A,J)
# -------------------------------------------------
names(medias_A_df) <- c(factor,'medias')
sumas_cuad <- data.frame('SCT'=SCI+SCE,
'SCI'=SCI,
'SCE'=SCE)
contraste <- data.frame('Factores'=factor,
'F'=F_stat,
'nivel crítico'=p_val)
return(list('medias'=medias_A_df,
'sumas cuadráticas'=sumas_cuad,
'contraste'=contraste,
'tamaño efecto'=effect_size(num_fact,N,
glE,
glA=glI,F_A=F_stat)))
}
two_way : Performs two-way ANOVA with fixed effects and assuming the same number of participants per combination of factor levels (balanced design). The procedure is based on the chapter on two-factor ANOVA in Pardo and San Martín (2015). The function provides a list with three dataframes containing the value of the F-statistic for each factor and for the interaction, the associated critical levels and three measures of effect size for each.
two_way <- function(num_fact,factor,vd,data){
N <- nrow(data) # Tamaño muestral
J <- nlevels(data[,factor[1]]) # Número de niveles del factor A
K <- nlevels(data[,factor[2]]) # Número de niveles del factor B
n <- N/(J*K) # Número de sujetos por combinación jk
# (se asume anova con diseño equilibrado)
# -------------------------------------------------
media_tot <- mean(data[,vd])
SCT <- sum((data[vd]-media_tot)^2)
glT <- N-1
# ------------------------------------------------- Estimador variabilidad intra
# basado en varianzas de cada combinación jk
varianzas <- aggregate(data[vd],
by=list(data[[factor[1]]],data[[factor[2]]]),
FUN=var)[[vd]]
SCE <- sum((n-1)*varianzas)
glE <- N-(J*K)
MCE <- SCE/glE
# ------------------------------------------------- Estimador variabilidad inter
# basado en medias del factor A
medias_A <- aggregate(data[vd],
by=list(data[[factor[1]]]),
FUN=mean)[[vd]]
SCa <- n*K*sum( (medias_A-media_tot)^2 )
glA <- J-1
MCa <- SCa/glA
F_stat_A <- MCa/MCE
p_val_A <- 1-pf(F_stat_A,glA,glE)
# ------------------------------------------------- Estimador variabilidad inter
# basado en medias del factor B
medias_B <- aggregate(data[vd],
by=list(data[[factor[2]]]),
FUN=mean)[[vd]]
SCb <- n*J*sum( (medias_B-media_tot)^2 )
glB <- K-1
MCb <- SCb/glB
F_stat_B <- MCb/MCE
p_val_B <- 1-pf(F_stat_B,glB,glE)
# ------------------------------------------------- Estimador variabilidad inter
# basado en medias del factor interacción
medias_inter_df <- aggregate(data[vd],
by=list(data[[factor[1]]],data[[factor[2]]]),
FUN=mean)
medias_inter <- medias_inter_df[[vd]] # el df es para la salida
SCab <- SCT-(SCa+SCb+SCE)
glAB <- (J-1)*(K-1)
MCab <- SCab/glAB
F_stat_AB <- MCab/MCE
p_val_AB <- 1-pf(F_stat_AB,glAB,glE)
# ------------------------------------------------- Ajuste condicional. Compara
# modelo aditivo e interactivo
aditiv_vs_inter <- ajuste_condicional(factor,vd,
SCT,SCa,SCb,SCE,
glT,glA,glB,glE)
# ------------------------------------------------- Salida
anova_plot(num_fact,factor,vd,data)
# -------------------------------------------------
names(medias_inter_df) <- c(factor,'medias') # nombrar adecuadamente df con medias
sumas_cuad <- data.frame('SCT'=SCT,
'SCa'=SCa,
'SCb'=SCb,
'SCab'=SCab,
'SCE'=SCE)
contraste <- data.frame('Factores'=c(factor,paste0(factor[1],'*',factor[2])),
'F'=c(F_stat_A,F_stat_B,F_stat_AB),
'nivel crítico'=c(p_val_A,p_val_B,p_val_AB))
tamano_efecto <- data.frame(contraste[1],
effect_size(num_fact,N,
glE,
glA,F_A=F_stat_A,
glB,F_B=F_stat_B,
glAB,F_AB=F_stat_AB))
return(list('ajuste_condicional'=aditiv_vs_inter,
'medias'=medias_inter_df,
'sumas cuadráticas'=sumas_cuad,
'contraste'=contraste,
'tamaño efecto'=tamano_efecto))
}
ajuste_condicional: It compares the fit of the simple model that includes only main effects (additive model) versus that of the more complex model, which includes the interaction component (interactive model). A non-statistically significant result indicates that there is no evidence that the interactive model produces a significant reduction in prediction errors compared to the simpler model. In this case a warning is given to the user, indicating that the ANOVA model generated may not be optimal. The procedure has been copied from Ato and Vallejo (2015) (p.138).
ajuste_condicional <- function(factor,vd,
SCT,SCa,SCb,SCE,
glT,glA,glB,glE){
SCE_aditivo <- SCT-(SCa+SCb)
glE_aditivo <- glT-(glA+glB)
SCE_inter <- SCE # SCE de modelo inter = SCT-(SCa+SCb+SCab)
glE_inter <- glE # glE de modelo inter = glT-(glA+glB+glAB)
F_stat <- ( (SCE_aditivo-SCE_inter)/(glE_aditivo-glE_inter) )/(SCE_inter/glE_inter)
p_val <- 1-pf(F_stat,(glE_aditivo-glE_inter),(glE_inter))
adit <- paste0(vd,'=',factor[1],'+',factor[2])
inter <- paste0(vd,'=',factor[1],'+',factor[2],'+',factor[1],'*',factor[2])
comparacion <- data.frame('modelo aditivo'=adit,
'modelo interactivo'=inter,
'F'=F_stat,
'nivel crítico'=p_val)
if (p_val>0.05) warning('Diferencia no significativa en grado de ajuste con
alfa=0,05. El modelo interactivo podría no ser apropiado')
return(data.frame('modelos'=c(adit,inter),
'F'=c(NA,F_stat),
'nivel crítico'=c(NA,p_val)))
}
effect_size : Calculates three measures of effect size for all factors involved in the ANOVA. Depending on the type of ANOVA (with 1 or 2 factors), it returns some formulas or others. All the formulas used have been copied directly from the chapters dedicated to ANOVA in Pardo and San Martín (2015). Factors are assumed to be fixed effects. Problem: when comparing results with those obtained with JASP software, it is observed that $\omega^2$ of the function is higher, the discrepancy being quite large in the case of two-factor ANOVA.
effect_size <- function(num_fact,N,
glE,
glA,F_A,
glB=NULL,F_B=NULL,
glAB=NULL,F_AB=NULL){
etas <- numeric()
omegas <- numeric()
deltas <- numeric()
for (gl_F in list(A=c(glA,F_A), B=c(glB,F_B), AB=c(glAB,F_AB))){
eta <- (gl_F[1]*gl_F[2])/(gl_F[1]*gl_F[2]+glE)
omega <- (gl_F[1]*(gl_F[2]-1))/(gl_F[1]*(gl_F[2]-1)+N)
delta <- sqrt( omega/(1-omega) )
etas <- c(etas,eta); omegas <- c(omegas,omega); deltas <- c(deltas,delta)
}
efs <- data.frame('delta Cohen' = deltas,
'eta cuadrado' = etas,
'omega cuadrado' = omegas)
return(efs)
}
An example: two-way ANOVA
This data set, “Heart Rate”, (example JASP file) provides heart rates of male and female runners and generally sedentary participants following 6 minutes exercise (800 observations). Does gender affect average heart rate? Does lifestyle (runners and non-runners) have an effect on heart rate? Is there an interactive effect of lifestyle and gender on heart rate?
Variables:
Gender - Participant’s gender (Female, Male).
Group - Group of ‘Runners’ (averaging more than15 miles per week) and ‘Control’ group (generally sedentary participant).
Heart.Rate - Heart rate after six minutes of exercise.
| Gender | Group | Heart.Rate |
|---|---|---|
| Female | Runners | 119 |
| Female | Runners | 84 |
| Female | Runners | 89 |
| Female | Runners | 119 |
| … | … | … |
ANOVA(factor=c('Gender','Group'),vd='Heart.Rate',data=data2)
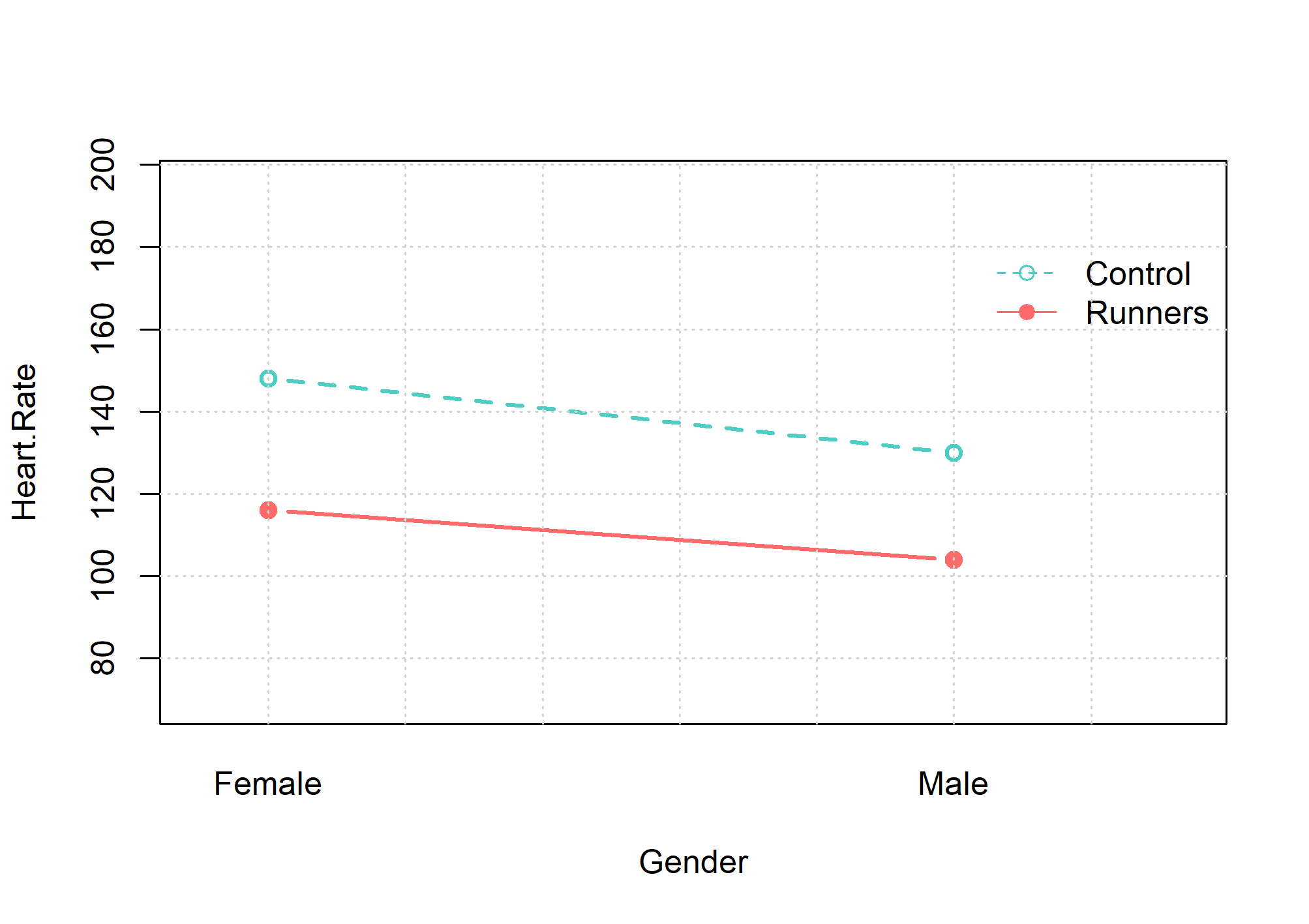
$ajuste_condicional
modelos F nivel.crítico
1 Heart.Rate=Gender+Group NA NA
2 Heart.Rate=Gender+Group+Gender*Group 7.409481 0.006629953
$medias
Gender Group medias
1 Female Control 148.000
2 Male Control 130.000
3 Female Runners 115.985
4 Male Runners 103.975
$sumas_cuadráticas
SCT SCa SCb SCab SCE
1 407985.9 45030.01 168432.1 1794.005 192729.8
$contraste
Factores F nivel.crítico
1 Gender 185.979949 0.000000000
2 Group 695.647040 0.000000000
3 Gender*Group 7.409481 0.006629953
$tamaño_efecto
Factores delta.Cohen eta.cuadrado omega.cuadrado
1 Gender 0.48085854 0.189392817 0.187800726
2 Group 0.93183089 0.466361694 0.464756575
3 Gender*Group 0.08950894 0.009222546 0.007948171
References
Pardo, A., & San Martín, R. (2015). Análisis de datos en ciencias sociales y de salud II. Editorial Síntesis.
Ato, M. & Vallejo, G. (2015). Diseños de investigación en Psicología. Ediciones Pirámide.